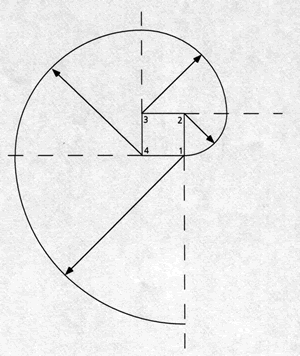LES SPIRALES À QUATRE CENTRES

Il existe deux catégories principales de spirales à quatre centres, les spirales géométriques ordinaires dont la progression est arithmétique, et les spirales logarithmiques dont la plus connue est sans doute la spirale dite de Fibonacci.

Spirale à quatre centres géométrique (progression arithmétique de raison 1)

Cette spirale est construite à partir d’un carré de 1 cm de côté (voir figure ci-dessous). Le long du côté 1-2 de ce carré, on construit un autre carré de même dimension dans lequel on trace un arce de cercle de centre 2.

Le long du côté 2-3 du carré original, on construit un carré de 2 cm de côté dans lequel on inscrit un nouvel arc de cercle de centre 3. Cet arc est donc relié au premier. Le long du côté 3-4 du carré de départ, on construit un nouveau carré de 3 cm de côté dans lequel on inscrit un 3ème arc de cercle de sommet 4, arc relié aux deux premiers. Enfin, on trace le long du côté 4-1 du carré de départ, un 4ème carré de 4 cm de côté, dans lequel on inscrit le dernier arc de cercle de sommet 1.

Le spirale à quatre centres (les points 1, 2, 3 et 4) est tracée.

| Haut de la page | Suite |

Dessin réalisé avec Illustrator

| Haut de la page | Suite |

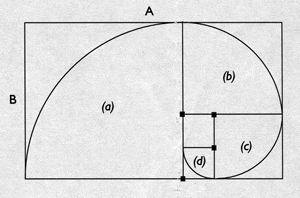
Spirale logarithmique, dite de Fibonacci

Cette spirale à quatre centres diffère de la précédente car sa progression est logarithmique et rétrograde, c’est-à-dire qu’on ne peut la construire qu’à l’envers, en partant de son dernier arc—en tous cas, je n’ai jamais réussi à la construire dans l’autre sens, mais je suis très mauvais en géométrie ! De plus, je n’ai jamais approfondi la question qui est, à mon avis, sans intérêt pour résoudre l’énigme.

La spirale de Fibonacci est aussi très particulière et très symbolique puisque sa construction fait appel au nombre d’or (1,618).

Soit donc un rectangle dont les côtés A et B respectent la proportion A ÷ B = 1,618. Ce rectangle peut être divisé en un carré (a) et un rectangle dont les côtés respecteront la même proportion.

Dans ce 1er carré (a), on inscrit un arc de cercle dont le centre est le sommet du carré qui lui est opposé. On divise ensuite le rectangle restant en un carré (b) et un nouveau rectangle dont les côtés respectent toujours la proportion du nombre d’or. On inscrit dans le 2ème carré un nouvel arc de cercle joignant le premier.

En poursuivant à l’identique [carrés (c) et (d)], on obtient une spirale qui, dans la figure ci-dessous, a quatre centres (matérialisés par les petits carrés noirs), mais qui pourrait en avoir davantage si l’on poursuivait selon le même principe.

Dessin réalisé avec Illustrator

| Haut de la page | Suite |

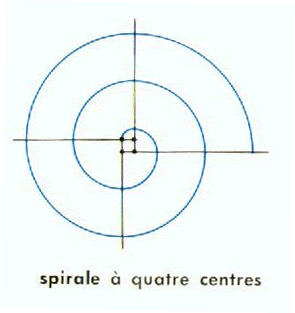
Enfin, voici une spirale à 4 centres des plus banales, mais intéressante en ce sens qu’elle a été trouvée par Velo (merci à lui) dans le Petit Larousse de 1978, date de la conception originale des énigmes... et je parie que la 500 ne fait pas partie partie de celles qui ont été « retouchées » en 1992 !

Conclusion

Il est très important de réaliser qu’une spirale « à quatre centres » n’est pas une figure géométrique particulière. Une spirale est une figure qu’on pourrait appeler « continue », en ce sens qu’en lui ajoutant des centres, on peut continuer à la développer à l’infini (ou vers le zéro pour la spirale de Fibonacci). Le fait de lui donner un 4ème centre ne lui attribue aucune qualité particulière qu’elle n’aurait pas encore eue avec seulement 3 centres, ou qu’elle perdrait si on lui en ajoutait un 5ème...

Pourquoi Max a-t-il alors précisé que la spirale de la 500 a 4 centres ? C’est là qu’il faut faire preuve d’astuce pour le comprendre, et résoudre intégralement l’énigme 500.

| Haut de la page | Retour à la 500 |