|
LES ÉNIGMES DE LA CHOUETTE D’OR
500
UT QUEANT LAXIS
A 2424-42-424-44-224-24-42-24, emprunte l’orthogonale.
Pour trouver la Spirale à quatre centres,
560.606 mesures, c’est loin.
Mais par le Méga, c’est un million de
fois moins.

|
Synthèse des madits du Fig-Mag :
|
L’une des deux lignes nécessaires pour construire
l’orthogonale est connue avant l’énigme 500.
L’orthogonale ne concerne directement que l'énigme
500.
560 606 mesures se comptent à partir de 2424-42-424-44-224-24-42-24.
La Spirale ne figure pas sur le visuel de cette énigme.
Le mot « méga » n’a qu’une
seule signification.
Le mot « mesure » apparaît dans
cette énigme, mais ce n’est pas la première
fois que vous rencontrez la mesure dans le jeu.
La longueur totale de la règle, l’écartement
des branches du compas et l’ombre de l’équerre
sur le visuel n’ont aucune importance. |
| Haut
de la page | Suite |
Cette énigme est assez
simple à trois conditions :
- Connaître la mesure trouvée en 780
(le pied métrique de 0,33 m, à mon avis) ;
- Avoir tracé en 470
la ligne Roncevaux-Bourges (éventuellement prolongée).
La synthèse Fig-Mag dit « connaître »
et non « tracer » pour rester en accord
avec le précepte selon lequel la carte n’est pas nécessaire
avant la présente énigme ; et surtout
- Avoir le déclic, l’astuce qui nous permettra en
fin d’énigme de comprendre ce qu’est la Spirale
à quatre centres.
Premier élément :
le 2424... etc. Nous inspirant de l’immanquable morse du visuel,
nous supposons que 2 vaut point et 4, trait. Loupé. Le bon
sens serait-il celui du contresens ici aussi ? Allez, on essaie
l’inverse. Avec 2 = trait et 4 = point, ça
marche et le décryptage donne : CARIGNAN, chef-lieu
de canton des Ardennes.
560.606 mesures, c’est
560.606 × 0,33 = 184.999,98 m que nous arrondissons à
185 km, en notant au passage que la précision nous confirme
que nous avons la bonne mesure.
Puisque Méga égale
million et qu’en passant par le Méga, la Spirale est
un million de fois moins loin, elle est donc à 185 km ÷
1.000.000 = 0,000185 km, soit 18,5 cm de Carignan. Quant au
« passage par le Méga » lui-même,
on comprend facilement qu’il s’agit dorénavant
d’utiliser une carte à l’échelle 1:1.000.000,
et l’I.S. FNAC
nous apprend que la bonne est la Michelin 989.
En étudiant cette carte,
nous réalisons, ô surprise ! que Carignan se trouve
sur le prolongement du trait joignant Roncevaux à Bourges...
Quand je dis « sur », j’exagère
un peu : en fait, de multiples tracés hyper-précis
sur de multiples 989 papier et plastifiées démontrent
que, si le trait passe exactement au milieu du petit polygone qui
figure la ville de Bourges sur cette carte, on laisse Carignan à
l’est de plusieurs millimètres. Il faut faire passer
notre
trait sur la partie sud-est de ce petit polygone pour atteindre
le petit rond symbolisant Carignan, mais cette légère
approximation est tout à fait tolérable : dans
une célèbre QR qu’il me semble légitime
d’appliquer au présent tracé, Max dit :
« En plein par l’Ouverture ou pas en plein par
l’Ouverture mais par l’Ouverture quand même, c’est
pareil ! ».
À la suite de multiples
débats, toujours, recommencés, sur la question de
savoir si Roncevaux, Bourges et Carignan sont ou non alignés,
j’ai résolu de mettre en ligne une
nouvelle page afin de démontrer que tel est bien le cas—tout
en sachant bien qu’il n’est de pire aveugle...
Il
y a un enseignement précieux à tirer de cela, à
savoir que la Chouette n’est pas (en tous cas au niveau des
tracés) d’une précision absolue.
Max a dit de nombreuses fois que le jeu est conçu pour s’accommoder
de légères imprécisions de tracés, sous-entendu
d’imprécisions des chercheurs dans leurs tracés...
En fait, il s’agit bien davantage d’imprécisions
dans la conception, imprécisions inévitables du
fait de la position des villes sur la carte, mais qu’il est
bon de garder en mémoire pour la suite...
Nous avons donc utilisé
le morse du visuel, et nous utiliserons la règle et l’équerre
pour tracer l’orthogonale. Nous remarquerons en passant que
les graduations de la partie visible de la règle, dont Max
a dit qu’elles étaient importantes, sont au nombre
de... 18,5, justement— nouvelle confirmation, indirecte celle-là,
de l’exactitude de la mesure. Mais la portée musicale
et sa clé de sol, qu’en faisons-nous ? Et
le titre, Ut queant laxis ?
| Haut
de la page | Suite |
|
Ut queant laxis
|
Cette phrase latine est le premier vers d’un chant liturgique
écrit au XIème siècle par le moine Gui
d’Arezzo, L’hymne à Saint-Jean Baptiste.
Cet hymne, dont les qualités musicales propres n’ont
rien d’époustouflant, est passé à
la postérité car chacun de ses vers commence
sur une des notes de la gamme, la 1ère syllable de
chaque vers ayant donné son nom à la note en
question (à l’exception du dernier où l’on
prend les initiales de Sancte et Iohannes) :
| Ut queant laxis |
-->
|
Ut (Do) |
| Resonare fibris |
-->
|
Ré |
| Mira gestorum |
-->
|
Mi |
| Famuli tuorum |
-->
|
Fa |
| Solve polluti |
-->
|
Sol |
| Labii reatum |
-->
|
La |
| Sancte Iohannes |
-->
|
Si |
Selon la même source (Quid), le si aurait été
ajouté à la fin du XVIème siècle
par Anselme de Flandre, le do n’apparaissant (et
devenant synonyme d’ut) qu’en 1673
avec l’Italien Bononcini.
À quoi cela nous sert-il dans l’énigme ?
Bonne question. L’hymne à Saint-Jean était-il
écrit en mesure 2/4 ? Je n’ai pas pu en trouver
confirmation. Et quand il le serait ? Max dit que le
titre doit être compris au début de l’énigme,
« afin d’avoir une idée sur la façon
de la décrypter », mais le morse du visuel
suffisait largement pour penser au code du même nom
et trouver Carignan... S’agit-il de comprendre que, dans
une mesure à 4 temps, il y a 4 noires (notes brèves)
ou 2 blanches (notes plus longues), ce qui nous permettrait
de déduire l’inversion 2 (petit chiffre) =
trait (signe long) et 4 (grand chiffre) = point (signe
court) ? Possible. Probable, même. Mais encore
une fois, avec un morse aussi « hénaurme »,
pas besoin d’en remettre une couche pour qu’on comprenne
de quoi il s’agit, et puisqu’il n’y a que deux
solutions possibles (2 = point ou 2 = trait), on
en a vite fait le tour !
Quant aux autres éléments du visuel (portée,
règle, équerre, compas), on peut les déplacer
séparément ou ensemble n’importe où
et n’importe comment, leurs positions et orientations
(absolues ou relatives) étant sans importance. La seule
chose qui compte, c’est que les graduations de la règle
ne soient pas masquées—nous avons vu plus haut
pourquoi.
|
| Haut
de la page | Suite |
|
Qu’y a-t-il
au bout de l’orthogonale ?
|
Si, comme moi, vous n’aviez jamais entendu parler de
spirale à quatre centres avant de chercher la Chouette,
cette lacune ne survivra pas à la 500 ! La première
chose est donc de savoir ce qu’est une telle spirale
par rapport, disons, à un banal escalier en colimaçon
ou à un colimaçon lui-même... Pour ce
faire, je vous propose de visiter ma page
Spirale.
Cet apprentissage étant fait, reste à savoir
si cette fameuse spirale doit être tracée ou
trouvée (sur la carte ou ailleurs). Max a toujours
refusé de le dire, et on pourrait penser que le compas
du visuel est là pour nous suggérer de la tracer.
Toutefois, le doute est, à mon sens, très vite
levé par un madit imparable selon lequel la spirale
est « toute entière sur l’orthogonale
à 560.606 mesures », et qu’en particulier,
« elle ne frôle pas l’orthogonale ».
En effet, si nous devons la tracer nous-mêmes, elle
aura forcément un certain développement, elle
occupera une certaine surface sur la carte. Elle ne sera donc
plus « toute entière » à
560.606 mesures... D’ailleurs, Max lâche quasiment
le morceau, car quand on lui dit que, géométriquement,
il est impossible de tracer une spirale toute entière
sur une droite, il répond : « À
vous de parvenir aux bonnes conclusions... mais bon, cette
conclusion n’est pas trop difficile à trouver ! ».
Postulons donc qu’il faut la trouver sur la carte, à
18,5 cm de Carignan sur la perpendiculaire au trait Roncevaux-Bourges-Carignan
tracée à partir de ce dernier lieu. Deux options
sont possibles : vers le sud-est et vers le nord-ouest.
C’est probablement ce que le compas veut nous suggérer :
l’orthogonale dans son intégralité est
le diamètre du cercle de centre Carignan, et pas seulement
l’un de ses rayons... ce qui est aussi une manière
d’entretenir le doute dans les esprits. Ici encore, Max
nous aide : « Si vous avez deux options, l’une
d’elles s’annulera forcément ! ».
L’orthogonale sud-est a la préférence
d’un grand nombre de chercheurs, car à son extrémité
se trouve le lieu qui a fait couler le plus d’encre parmi
les chasseurs de Chouette : Dabo.
| Haut
de la page | Suite |
|
|
Dabo
|
Dabo, petit village de Moselle à la limite du Bas-Rhin,
divise les chasseurs de Chouette depuis des années.
Il est en effet doté d’un très remarquable
rocher surmontée d’une chapelle dédiée
à Saint-Léon.
Or, ce rocher, photographié sous un certain angle
par une nuit sans lune (bon, je plaisante, disons donc « dans
certaines conditions d’éclairement »!),
fait un très présentable NNP (voir la 600),
comme le montre la photo ci-dessous, empruntée au site
de Mickey (www.ilotresor.com),
chef de file de l’école daboïste et sur lequel
vous pourrez trouver toutes les informations possibles et
imaginables sur Dabo. Mickey est allé à Dabo
des dizaines de fois et en sait davantage sur le sujet que
tout le personnel de l’Office de Tourisme réuni (voir
aussi ma Page
Dabo) !

Si Dabo est le NNP, il est bien tentant de voir dans la chapelle
Saint-Léon la Nef encalminée de la 560...
et comme justement, la route d’accès au rocher
est en spirale, comment résister à la tentation
d’y voir « la » Spirale...? De
plus, Dabo est aussi le point d’atterrissage de la flèche
d’Apollon dans la 420 !!
Oui, comment résister ? De très nombreux
chasseurs ne l’ont pas fait et si j’ai, personnellement,
choisi de le faire, c’est, bien longtemps avant d’avoir
résolu la 500, en raison d’une conviction très
forte : nous sommes engagés dans une chasse de
très longue haleine, composée de très
peu d’énigmes mais qui nous balade d’un bout
à l’autre de la France, voire hors des frontières ;
nous passons dans des lieux où nous ne nous attardons
pas, et lorsque nous devons y revenir, on nous le dit et ces
lieux ou concepts prennent une importance considérable
(l’Ouverture, la Lumière, le NNP/Nef).
Et dans ce contexte, fait tout ensemble de concision et d’ampleur,
où l’auteur n’a ni la place ni sans doute
le goût de se répéter, Dabo serait à
la fois le NNP, la Nef, la Spirale et le point de chute
de la flèche d’Apollon, ces deux derniers lieux
étant au surplus donnés par deux énigmes
successives qui sont, en tous cas de prime abord, parmi les
plus simples du jeu ?
C’est trop. D’abord, il est intellectuellement
impensable que Max ait concentré autant de concepts
sur un seul lieu ; c’est ce que les Anglo-Saxons
appellent de l’overkill, comme balancer 10 bombes
nucléaires là où une suffirait à
anéantir toute vie. Ensuite, à supposer qu’un
lieu unique ait une telle importance et soit l’aboutissement
d’autant d’énigmes (40 % du total!),
Max ne serait pas allé le « crier sur les
toits » comme on peut considérer qu’il
le fait dans la 500 et dans la 420...
en faisant trouver Dabo par des solutions aussi simples (à
l’échelle de la Chouette, bien sûr).

Une autre photo du rocher de Dabo... dans certaines conditions
d’éclairement :o)
| Haut
de la page | Suite |
Dabo, donc, n’est pas la Spirale. D’ailleurs, comment
démontrer qu’une route en spirale, si parfaite
soit-elle (et ce n’est pas le cas de celle de Dabo) est
à quatre centres ? Même le plus expert
des daboïstes n’a jamais pu expliquer pourquoi la
spirale de la route de Dabo serait à quatre centres
plutôt qu’à 3, 5 ou 10, ni où se
trouveraient les 4 centres en question !
J’ai bien pris note du fait que Max n’a jamais
voulu donner pour Dabo une localisation négative comme
il a pu le faire pour le Mont Saint-Michel ou la forêt
de Brocéliande (voir la page
I.S.), mais c’est à mon sens, tout simplement,
pour ne pas décourager les très nombreux chasseurs
qui y croient dur comme fer. Réflexe un peu « commercial »,
les chercheurs ayant aussi été des clients à
l’époque du 3615
MAXVAL ? C’est possible, mais comment l’en
blâmer ? Max est un auteur professionnel qui vit
de ses chasses, et après tout personne n’était
obligé d’aller lui poser des questions par Minitel !
Cela étant, et même sans localisation négative
formelle, Max a quand même bien voulu lâcher,
à propos de la Spirale, que « à ce
niveau, certains chasseurs se sont peut-être laissés
entraîner sur une fausse piste... ». C’est,
à mon avis, amplement suffisant.
| Haut
de la page | Suite |
|
Bon, mais alors,
la Spirale, c’est quoi ?
|
Je me suis longtemps refusé
à indiquer publiquement sur ce site quelle était,
selon moi, la Spirale. J’expliquais ici même qu’ayant
pris totalement congé des chasses au trésor
entre janvier 2000 et janvier 2002, et être resté
au total plus de trois ans sans toucher à la Chouette,
j’essayais de « rattraper mon retard »
et ne désirais donc pas dévoiler cet élément.
Depuis, les choses ont évolué. Ma vie personnelle
et mes autres occupations (dont mes occupations « para-chouttesques »,
telles que le tournage du film La
Grande Aventure de la Chouette d’Or), font
que, depuis près d’un an (j’écris
ceci en novembre 2004), je n’ai plus le temps de chercher
sérieusement la Chouette.
De plus, en lisant le forum, je vois de temps à autre
quelqu’un faire de la publicité pour ce que je
considère être la « bonne »
Spirale : il n’y a donc plus vraiment de raison
pour moi de garder le silence.
Reprenons donc les choses au début, en nous aidant
des madits et de quelques photographies. Que cherchons-nous ?
Nous cherchons une entité baptisée par Max
« Spirale à quatre centres »,
qui est toute entière sur l’orthogonale et à
18,5 cm de Carignan sur la carte Michelin 989. Cette notion
d’entièreté exclut tout traçage
sur la carte, puisqu’une spirale tracée, du seul
fait de son développement, ne serait plus toute entière
sur l’orthogonale (qui est une droite), mais en déborderait
largement. La Spirale doit donc
être trouvée—pas tracée.
Max précise que la Spirale « n’est
pas vraiment difficile à trouver » et qu’il
y faut « autant d’astuce que de logique ».
Prenons donc la carte et regardons
où les tracés nous conduisent...
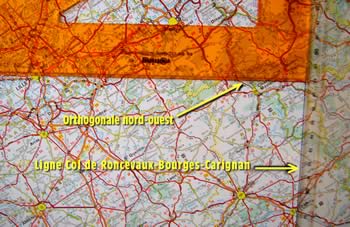
Mise en place de l’orthogonale (partie nord-ouest)
Pour voir cette photo en grand format, cliquer dessus. Le
lien de retour vous
ramènera directement ici (procédure applicable
à toutes les images ci-après).
ATTENTION : les
photos grand format seront longues à télécharger !
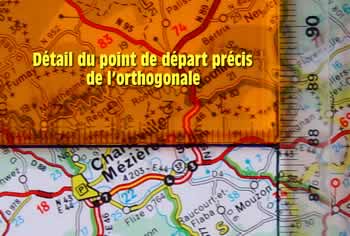
On distingue sous la règle transparente l’appellation
« Carignan ».
Une fois l’orthogonale tracée
à l’aide de l’équerre vers le nord-ouest,
prolongeons-la vers le sud-est pour disposer des deux « branches »
complètes, sachant qu’on n’emprunte l’orthogonale
que dans une seule direction puisqu Max précise :
« Si vous avez deux options, l’une d’elles
s’annulera forcément » ; ou encore :
« Procédez par élimination et vous
trouverez la bonne réponse assez rapidement ».
À 18,5 cm de Carignan vers le sud-est, voici ce que
j’obtiens :
Le résultat côté Dabo n’est donc
pas très convaincant graphiquement. On aurait pu éventuellement
l’admettre si le raisonnement l’avait
été, convaincant, mais ce n’est pas le
cas, comme on l’a exposé plus haut.
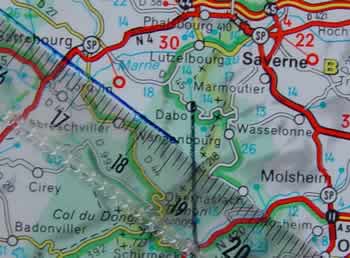
Regardons donc ce qu’on trouve
à 18,5 cm de Carignan vers le nord-ouest :
Le point d’arrivée est donc situé dans
le « pâté jaune » de l’agglomération
lilloise. Regardons de plus près sur une carte d’approche
au 1:200.000 :
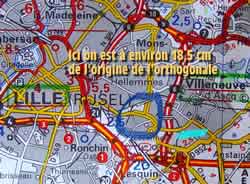
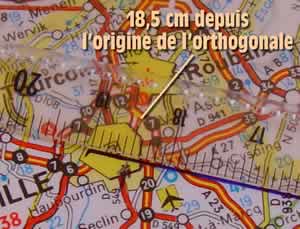
Comme on le voit sur l’agrandissement,
18,5 cm depuis Carignan nous emmènent en bordure de
l’agglomération lilloise, à proximité
immédiate, non pas de Villeneuve d’Ascq, mais
d’un quartier péri-urbain dénommé simplement
Ascq, qui était encore un village distinct la fin de
la Seconde Guerre mondiale, comme le montre la photo ci-dessous,
prise au Mémorial de Caen.

À mon sens, c’est ce lieu, Ascq, qui représente
dans la Chouette ce que Max Valentin appelle « Spirale
à quatre centres ». Bien entendu, il n’y
a à Ascq, autant que je le sache, aucune spirale physique
mais cela est sans importance : appeler un lieu « Spirale
à quatre centres », c’est lui donner
un acception symbolique dans le cadre du jeu, sans référence
nécessaire à une réalité physique
(tout comme Bourges a été baptisée « Ouverture »).
Max voulait nous faire trouver Ascq, et pour y parvenir il
a utilisé un cryptage très simple (l’acrostiche),
légèrement compliqué par le mélange
des lettres mais qui, surtout, requiert de l’astuce.
En effet, mis en présence d’un concept géométrique
très précis et abouti tel qu’une spiale
à quatre centres, il faut savoir s’en abstraire
complètement et réfléchir out
of the box, comme disent nos amis Anglo-Saxons—en
dehors des étroites limites de la petite boîte
dans laquelle l’auteur a voulu nous enfermer.
Ce n’est qu’à cette condition qu’on
peut trouver la solution et cette démarche, me semble-t-il,
illustre très bien la manière de faire de Max,
et la démarche à adopter pour espérer
trouver la Chouette.
Ascq est donc une solution astucieuse, trouvable même
si on ne connaît pas la mesure (il suffit de suivre
l’orthogonale et de voir à poximité de
quoi elle passe), n’est pas vraiment difficile à
trouver... Bref, cette solution est en conformité parfaite
avec les madits existant sur le sujet. De plus, utilier l’image
d’une spirale pour se référer à
Ascq permettait à Max de solidifier la fausse piste
de Dabo.
L’argument ultime, qui forge définitivement
ma conviction, est très intéressant car de nature
psychologique et donc propre à « trahir »
l’auteur sans qu’il y puisse grand-chose.
Voici quel est cet argument : pendant des années,
Max a passé des dizaines de milliers d’heures
à taper sur un clavier de Minitel pour répondre
aux questions des chercheurs. Ceux qui ont pratiqué
le Minitel savent à quel point ce clavier était
peu confortable et rébarbatif à utiliser ;
pourtant, Max était obligé de s’en servir
de manière extrêmement intensive, jour après
jour... Les chercheurs avaient donc inventé toute une
série d’abréviations, à la fois
pour rester connectés le moins longtemps possible (car
cela finissait par coûter fort cher), mais aussi pour
pouvoir faire tenir des questions parfois longues et complexes
dans un espace de quelques lignes de 40 caractères.
Max connaissait fort bien ces abréviations (il en
fit même un lexique dans les solutions du Trésor
d’Orval), parmi lesquelles figurait bien sûr
« SAQC » pour « Spirale à
quatre centres ». Et pourtant... pas une fois Max
n’a utilisé cette abréviation ! Pas
une.
Ou plutôt si : une fois. Pas SAQC (quand même !),
mais S4C. Et quelle a été sa réaction
quand on le lui a fait remarquer ? « J’ai
eu tort ! » s’est-il exclamé.
Et pourquoi diable aurait-il donc eu tort ? Tort d’avoir,
sans réfléchir, parce qu’il était
fatigué et a repris machinalement dans sa réponse
l’abréviation de celui à qui il répondait,
utilisé machinalement une expression bien trop proche
de la solution de l’énigme...
  
Détail du tableau original photographié chez
Michel Becker
| Haut
de la page |
|
|











